用SDL弹奏五线谱来演示波形声音的生成的一个例子

陪她去流浪桃子 2019年03月04日编辑阅读次数：3308

我在文章《波形声音编程的一点笔记》中简短地描述了声音是如何产生的，声音与函数波形的关系。

这篇文章我用一个实际的例子来模拟产生声音———用Go语言+SDL音频来播放一段五线谱的曲子。

注意：阅读本文需要读者有一定的音乐理论知识（即乐理），还要求懂一点钢琴。

提示：文章包含数学公式，通过RSS直接阅读的读者暂不能正确显示，请访问原文。

提示：这篇文章是初稿，可能包含较多的知识性错误，望读者指正。

初始化SDL库音频子系统

SDL支持多种子系统：音频、视频、键盘、控制器等。这里我只需要初始化音频即可，代码如下：

1
2
3
4
5
6
7
8
9


// 初始化音频设备
func initAudio() {
	var err error

	// 仅初始化音频子系统
	if err = sdl.Init(sdl.INIT_AUDIO); err != nil {
		panic(err)
	}
}

初始化音频详细参数

上面的代码只是进行了最简单的初始化操作———初始化SDL音频子系统。

接下来还需要一步详细的初始化：告诉SDL音频本身相关的参数，包括：通道数、采样率、量化数据格式、采样数、数据回调。

以下是音频参数结构，部分必要的参数已加上注释：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


// AudioSpec contains the audio output format.
// (https://wiki.libsdl.org/SDL_AudioSpec)
type AudioSpec struct {
	Freq     int32          // 采样率（每秒采样数）
	Format   AudioFormat    // 音频数据格式
	Channels uint8          // 音频通道个数
	Silence  uint8          // 
	Samples  uint16         // 音频缓冲区大小（单位：采样数）
	_        uint16         // 
	Size     uint32         // 
	Callback AudioCallback  // 当音频设备需要更多的音频数据的时候，回调此函数
	UserData unsafe.Pointer // 传递给回调函数的自定义参数
}

在这篇文章中，我加入初始化后参数后的代码如下。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


// 这是采样频率
// 44KHz已经很好了
const sampleHz = 44100

// 每秒钟的音符数
const notesPerSecond = 6

// 每个音符的采样数
const samplesPerNote = sampleHz / notesPerSecond

//export WaveOut
// 这个函数是SDL的音频子系统需要我们提供更多的音频数据的时候回调的
// 注意，这是一个cgo回调函数。注意最开始的函数export声明
func WaveOut(userdata unsafe.Pointer, stream *C.Int8, length C.int) {

}

func initAudio() {
	var err error

	// 仅初始化音频子系统
	if err = sdl.Init(sdl.INIT_AUDIO); err != nil {
		panic(err)
	}

	// 音频参数
	spec := &sdl.AudioSpec{
		Freq:     sampleHz,      // 采样率(每秒采样数)
		Format:   sdl.AUDIO_F32, // 量化数据格式，这个例子使用浮点类型
		Channels: 2,             // 通道数，立体声。分别对应五线谱的高低音谱表
		Samples:  samplesPerNote,
		Callback: sdl.AudioCallback(C.WaveOut),
	}
	if err = sdl.OpenAudio(spec, nil); err != nil {
		panic(err)
	}
}

其中出现了几个常量定义：采样率，每秒钟的音符数，计算得出的每个音符的采样数。我设置的这些值的具体意义我在下一节解释。

最重要的是那个WaveOut回调函数，这个函数在被回调时由我们往缓冲区里面填充音频数据。

音频参数填写好后，调用sdl.OpenAudio打开音频设备，然后调用sdl.PauseAudio播放音频，在等待播放完毕后（代码中没有体现出来），调用sdl.CloseAudio关闭音频。

其实这时候代码已经可以跑起来了。因为没有提供音频数据，所以并不会产生任何声音而已。

音频参数值的计算

这里以我比较喜欢的久石让的Summer为例，取谱子的前几节，以下是谱子。（完整谱子）

Summer

先看一下谱子的基本信息：

两个升号，D调
$\frac{4}{4}$ ，4分音符为一拍，每小节4拍
，每分钟90个4分音符的拍速

由于谱子中最小的音符为16分音符，为简化起见，此文章的代码每次弹奏一个16分音符。

那么，8分音符分成2个16分音符弹奏，4分音符分成4个16分音符弹奏。依此类推。

4分音符换成16分音符，得：每分钟360个16分音符，即每秒钟6个。这就是上面

1
2


// 每秒钟的音符数
const notesPerSecond = 6

的由来。再由于我将采样率定义为：

1
2
3


// 这是采样频率
// 44KHz已经很好了
const sampleHz = 44100

所以，得出每个音符的采样数为：

1
2


// 每个音符的采样数
const samplesPerNote = sampleHz / notesPerSecond

钢琴的模拟

键盘

钢琴一共有88个键（ $3 + 12 \times 7 + 1 = 88$ ），分为9组。从左到右音的频率逐渐升高。长下面这样：

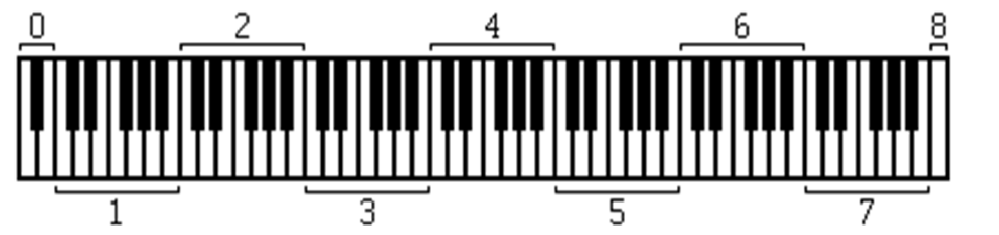
Full Piano Keyboard — Piano Notes and the Keys they Correspond to

中间7组，他们每组都长下面这样（最后一个灰色的C请忽略，没找到更好的图）：

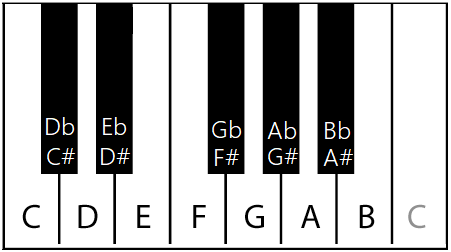
一共12个键。7个白键 + 5个黑键。每个键的名字（音名）已标注。最左边的第0组只包含上图的右边3个键（A，A♯/B♭，B）。最右边的第8组只包含上图的左边一个键（C）。整个键盘就由上图循环排布而成。

音高

音名相同的最近两个键（的音程）称为一个八度（octave）。它们的频率（声音是振动产生的）之比正好为 $1 : 2$ （右边的高）。比如：图中的两个C就是一个八度，它们的频率之比为 $1 : 2$ 。任意一个八度内共有12个键，它们把这2倍的频率之比等比均分（十二平均律由此而来）（人的耳朵对两个音之间的频率之比敏感，而不是之差）。

因此，它们的频率构成一个等比数列，不妨设其公比为 $q$ ，那么： $q = 122$ 。

假定C的频率为 $f$ 。那么，可以据此推出其左右的部分音的音高（频率）：

音名	频率
A	$f \times q^{- 3}$
A♯	$f \times q^{- 2}$
B	$f \times q^{- 1}$
C（假定音）	$f \times q^{0}$
C♯	$f \times q^{1}$
D	$f \times q^{2}$
D♯	$f \times q^{3}$
E	$f \times q^{4}$
F	$f \times q^{5}$
F♯	$f \times q^{6}$
G	$f \times q^{7}$
G♯	$f \times q^{8}$
A	$f \times q^{9}$
A♯	$f \times q^{10}$
B	$f \times q^{11}$
C	$f \times q^{12}$
C♯	$f \times q^{13}$

在国际上，第4组的A（从最左往右数，第49个键）被规定为 $440 Hz$ ，它被称作标准音。如果要写一个函数，根据A求第n个键的频率。这个函数大概长这样： $f (n) = 440 \times (122)^{n - 49} = 440 \times 2^{\frac{n - 49}{12}}$ . 其中： $n \in N_{+}, 1 \leq n \leq 88$ 。

写成代码，那么它长这样：

1
2
3
4


// 计算出第n个键的频率
func keyFreq(n int) float64 {
	return math.Pow(2, float64(n-49)/12.0) * 440
}

根据以上计算各个键的频率 $f$ 的计算公式，外加上预设的采样数 $s am pl eHz$ ，可以得到每次采样时和上一次采样时的相位差： $Δ p = \frac{2 π \times f}{s am pl eHz}$ 。

这些参数都是常数，可以在一开始就计算出来：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


// 键的相关参数
var keyParams [1 + 88]struct {
	freq   float64
	dPhase float64
}

// 计算各个键的参数
func initKeyParams() {
	keyParams[0].freq = 0
	keyParams[0].dPhase = 0

	for i := 1; i <= 88; i++ {
		f := keyFreq(i)
		keyParams[i].freq = f
		keyParams[i].dPhase = 2 * math.Pi * f / sampleHz
	}
}

键盘的表示

在我的这篇文章中，钢琴的88个键被编号为 $1 - 88$ ，用 $0$ 表示16分休止符（不按任何键）。

键的类型被定义为如下：

1
2


// Key 是键的类型定义
type Key int

休止符被定义成这样（主要是为了后面看起来好看一点）：

1
2


// 休止符
const __ = Key(0)

第1组键的C的编号为 $4$ 。依次定义出同一个八度内的其它音：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


// 同一个八度内的音名
const (
	Cn Key = iota + 4
	Cs
	Dn
	Ds
	En
	Fn
	Fs
	Gn
	Gs
	An
	As
	Bn
)

n表示白键上的音，s代表对应升高半音的音（靠得最近那个）。

然后，可以写一个函数，根据音名和组号来确定这个音名对应的键的具体编号：

1
2
3
4
5
6
7


// K 用来根据音名和组号求其键的编号
func K(key Key, group int) Key {
	if key == __ {
		return 0
	}
	return key + Key((group-1)*12)
}

前面介绍keyParams的时候，我把它定义成了 $1 + 88$ 的大小，多出来的一个就是用来表示不按下任何键的，也即这个键等于__的时候。

五线谱数据的采集

这篇文章采集了前面提到的Summer的第 $3 - 8$ 小节为例。要会看五线谱才会看明白我下面的代码哦！数据如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


// 待弹奏的一段五线谱
var notesToPlay = [6][2][16]Key{
	// 第3小节
	{
		{K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0)},
		{K(Bn, 2), K(Bn, 2), K(Fs, 3), K(Fs, 3), K(Bn, 3), K(Bn, 3), K(Fs, 3), K(Fs, 3), K(Gn, 2), K(Gn, 2), K(Dn, 3), K(Dn, 3), K(Gn, 3), K(Gn, 3), K(Dn, 3), K(Dn, 3)},
	},
	// 第4小节
	{
		{K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(An, 4), K(Dn, 5), K(En, 5), K(Fs, 5)},
		{K(An, 2), K(An, 2), K(En, 3), K(En, 3), K(An, 3), K(An, 3), K(En, 3), K(En, 3), K(Dn, 3), K(Dn, 3), K(An, 3), K(An, 3), K(Dn, 4), K(Dn, 4), K(An, 3), K(An, 3)},
	},
	// 第5小节
	{
		{K(En, 5), K(En, 5), K(Dn, 5), K(Dn, 5), K(Dn, 5), K(Dn, 5), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(An, 4), K(Dn, 5), K(En, 5), K(Fs, 5)},
		{K(Bn, 2), K(Bn, 2), K(Fs, 3), K(Fs, 3), K(Bn, 3), K(Bn, 3), K(Fs, 3), K(Fs, 3), K(Gn, 2), K(Gn, 2), K(Dn, 3), K(Dn, 3), K(Gn, 3), K(Gn, 3), K(Dn, 3), K(Dn, 3)},
	},

	// 第6小节
	{
		{K(En, 5), K(En, 5), K(Dn, 5), K(En, 5), K(En, 5), K(Fs, 5), K(Fs, 5), K(Fs, 5), K(Fs, 5), K(Fs, 5), K(Fs, 5), K(Fs, 5), K(An, 4), K(Dn, 5), K(En, 5), K(Fs, 5)},
		{K(An, 2), K(An, 2), K(En, 3), K(En, 3), K(An, 3), K(An, 3), K(En, 3), K(En, 3), K(Dn, 3), K(Dn, 3), K(An, 3), K(An, 3), K(Dn, 4), K(Dn, 4), K(An, 3), K(An, 3)},
	},
	// 第7小节
	{
		{K(En, 5), K(En, 5), K(Dn, 5), K(Dn, 5), K(Dn, 5), K(Dn, 5), K(Dn, 5), K(Dn, 5), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(An, 4), K(Dn, 5), K(En, 5), K(Fs, 5)},
		{K(Bn, 2), K(Bn, 2), K(Fs, 3), K(Fs, 3), K(Bn, 3), K(Bn, 3), K(Fs, 3), K(Fs, 3), K(Gn, 2), K(Gn, 2), K(Dn, 3), K(Dn, 3), K(Gn, 3), K(Gn, 3), K(Dn, 3), K(Dn, 3)},
	},
	// 第8小节
	{
		{K(En, 5), K(En, 5), K(Dn, 5), K(En, 5), K(En, 5), K(An, 5), K(An, 5), K(Fs, 5), K(Fs, 5), K(Fs, 5), K(Fs, 5), K(Fs, 5), K(__, 0), K(__, 0), K(__, 0), K(__, 0)},
		{K(An, 2), K(An, 2), K(En, 3), K(En, 3), K(An, 3), K(An, 3), K(En, 3), K(En, 3), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0), K(__, 0)},
	},
}

解释：每小节16个音，每小节两个声部（通道），共6个小节。这就是数组的3个下标16、2、6的由来。

手动采集真是累到不行！

生成音频数据 / 再看回调函数

这一节是本文的重点了。音频设备需要音频数据的时候，SDL会回调我们之前提供的回调函数。再来看看这个回调函数：

1
2
3


func WaveOut(userdata unsafe.Pointer, stream *C.Int8, length C.int) {

}

对入参的解释

userdata

这个参数用于传递用户自定义的数据，是一个指针。它是在初始化时调用sdl.OpenAudio时指定的，SDL原样传递过来。
stream

音频数据缓冲区，是一个指向int8的指针。我们把计算生成来的数据填到这里面。具体的格式和大小由初始化时指定的参数而定。

这是一个C语言的缓冲区，如果要在Go里面直接使用，需要借助反射将其转换成Go可直接读写的切片类型。转换代码如下：
1 2 3

n := int(length) hdr := reflect.SliceHeader{Data: uintptr(unsafe.Pointer(stream)), Len: n, Cap: n} buf := *(*[]C.Float)(unsafe.Pointer(&hdr))
length

缓冲区的大小（单位：字节）。

数据生成函数的原型

从前面的小节知道，我将回调函数的缓冲区大小刚好设置成了一个音符的大小。这样一来，我们可以一次性计算出一个音符的全部数据。

数据怎么生成呢？计算出声音波形函数在某时刻的响应即可。我在一开始的时候已经把每一个键在当前采样数下的相位差计算出来了，那么，万事俱备。

等等！我还没定义如何根据一个相位计算出响应的函数的原型。我把它叫作WaveFunc，原型如下：

1
2


// WaveFunc 根据一个相位输出当前波的响应
type WaveFunc func(float64) float64

同时还定义了另外一个原型：

1
2


// PhaseFunc 输入两个相位，输出两个指定格式的音频数据
type PhaseFunc func(float64, float64) (float32, float32)

音频数据的生成

这段代码的核心如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


var key0 Key
var key1 Key

var phase0 float64
var phase1 float64

for sample := 0; sample < samplesPerNote; sample++ {
	value0, value1 := phaseFunc(phase0, phase1)

	buf[sample*2+0] = C.Float(value0)
	buf[sample*2+1] = C.Float(value1)

	phase0 += keyParams[key0].dPhase
	phase1 += keyParams[key1].dPhase
	if phase0 >= 2*math.Pi {
		phase0 = 0
	}
	if phase1 >= 2*math.Pi {
		phase1 = 0
	}
}

下面是解释：

这个循环循环samplesPerNote那个多次，即一个音符的采样数；
对每一次采样，调用响应函数phaseFunc（类型为PhaseFunc）生成单个音频数据；
将音频数据写入缓冲区中；
相位值偏移到下一个值（周期规定在 $2 π$ 内）。

各种生成函数

现实世界声音的波的生成函数是极其复杂的，非常难模拟出来。但根据傅立叶变换，复杂的波形经过时域到频域的变换后，可以变成若干简单的波形叠加而来。那么，我就用最简单的波来做实验了。

正弦波

1
2
3
4


// SineWave 正弦波
func SineWave(phase float64) float64 {
	return math.Sin(phase)
}

线性波

1
2
3
4


// LinearWave 线性波
func LinearWave(phase float64) float64 {
	return 1 / math.Pi * phase
}

三角波

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


// TriangleWave 三角波
func TriangleWave(phase float64) float64 {
	switch {
	case phase < math.Pi:
		return 1 / math.Pi * phase
	default:
		// f(phase) == f(2Pi-phase), phase > Pi
		return 1 / math.Pi * (2*math.Pi - phase)
	}
}

方波

duty是方波的占空比。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


// NewPulseWaveFunc 方波
func NewPulseWaveFunc(duty float64) WaveFunc {
	t := 2 * math.Pi * duty
	return func(phase float64) float64 {
		switch {
		case phase < t:
			return 1
		default:
			return -1
		}
	}
}

PhaseFunc 的一个实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


// 是否各通道独立弹奏（否则合并）
var sepChannel = true

// 全局生成函数（会在回调里面调用）
var phaseFunc PhaseFunc

// initPhaseFunc 初始化生成函数
func initPhaseFunc() {
	waveFunc0 := SineWave
	waveFunc1 := SineWave

	phaseFunc = func(phase0 float64, phase1 float64) (float32, float32) {
		var value0, value1 float64
		if !sepChannel {
			value0 = (waveFunc0(phase0) + waveFunc0(phase1)) / 2
			value1 = (waveFunc1(phase0) + waveFunc1(phase1)) / 2
		} else {
			value0 = waveFunc0(phase0)
			value1 = waveFunc1(phase1)
		}
		return float32(value0), float32(value1)
	}
}

弹奏时的一些控制

为了让弹奏看起来更加“友好”，我加入了打印音符、小节控制、循环弹奏、自动退出等功能。但是这些应该算是锦上添花的功能，所以不再细细阐述。

实际弹奏的一些小问题

由于波形比较简单，声线并不是“特别”好听；
由于音频数据是在回调函数里面及时生成的，不够快，因为没有缓冲生成。可能听起来有些断断续续；

打印出来的谱子

$ go run main.go
-----------
𝄢:B2  𝄞:---
𝄢:B2  𝄞:---
𝄢:F3# 𝄞:---
𝄢:F3# 𝄞:---
···········
𝄢:B3  𝄞:---
𝄢:B3  𝄞:---
𝄢:F3# 𝄞:---
𝄢:F3# 𝄞:---
-----------
𝄢:G2  𝄞:---
𝄢:G2  𝄞:---
𝄢:D3  𝄞:---
𝄢:D3  𝄞:---
···········
𝄢:G3  𝄞:---
𝄢:G3  𝄞:---
𝄢:D3  𝄞:---
𝄢:D3  𝄞:---
-----------
𝄢:A2  𝄞:---
𝄢:A2  𝄞:---
𝄢:E3  𝄞:---
𝄢:E3  𝄞:---
···········
𝄢:A3  𝄞:---
𝄢:A3  𝄞:---
𝄢:E3  𝄞:---
𝄢:E3  𝄞:---
-----------
𝄢:D3  𝄞:---
𝄢:D3  𝄞:---
𝄢:A3  𝄞:---
𝄢:A3  𝄞:---
···········
𝄢:D4  𝄞:A4 
𝄢:D4  𝄞:D5 
𝄢:A3  𝄞:E5 
𝄢:A3  𝄞:F5#
-----------
𝄢:B2  𝄞:E5 
𝄢:B2  𝄞:E5 
𝄢:F3# 𝄞:D5 
𝄢:F3# 𝄞:D5 
···········
𝄢:B3  𝄞:D5 
𝄢:B3  𝄞:D5 
𝄢:F3# 𝄞:---
𝄢:F3# 𝄞:---
-----------
𝄢:G2  𝄞:---
𝄢:G2  𝄞:---
𝄢:D3  𝄞:---
𝄢:D3  𝄞:---
···········
𝄢:G3  𝄞:A4 
𝄢:G3  𝄞:D5 
𝄢:D3  𝄞:E5 
𝄢:D3  𝄞:F5#
-----------
𝄢:A2  𝄞:E5 
𝄢:A2  𝄞:E5 
𝄢:E3  𝄞:D5 
𝄢:E3  𝄞:E5 
···········
𝄢:A3  𝄞:E5 
𝄢:A3  𝄞:F5#
𝄢:E3  𝄞:F5#
𝄢:E3  𝄞:F5#
-----------
𝄢:D3  𝄞:F5#
𝄢:D3  𝄞:F5#
𝄢:A3  𝄞:F5#
𝄢:A3  𝄞:F5#
···········
𝄢:D4  𝄞:A4 
𝄢:D4  𝄞:D5 
𝄢:A3  𝄞:E5 
𝄢:A3  𝄞:F5#
-----------
𝄢:B2  𝄞:E5 
𝄢:B2  𝄞:E5 
𝄢:F3# 𝄞:D5 
𝄢:F3# 𝄞:D5 
···········
𝄢:B3  𝄞:D5 
𝄢:B3  𝄞:D5 
𝄢:F3# 𝄞:D5 
𝄢:F3# 𝄞:D5 
-----------
𝄢:G2  𝄞:---
𝄢:G2  𝄞:---
𝄢:D3  𝄞:---
𝄢:D3  𝄞:---
···········
𝄢:G3  𝄞:A4 
𝄢:G3  𝄞:D5 
𝄢:D3  𝄞:E5 
𝄢:D3  𝄞:F5#
-----------
𝄢:A2  𝄞:E5 
𝄢:A2  𝄞:E5 
𝄢:E3  𝄞:D5 
𝄢:E3  𝄞:E5 
···········
𝄢:A3  𝄞:E5 
𝄢:A3  𝄞:A5 
𝄢:E3  𝄞:A5 
𝄢:E3  𝄞:F5#
-----------
𝄢:--- 𝄞:F5#
𝄢:--- 𝄞:F5#
𝄢:--- 𝄞:F5#
𝄢:--- 𝄞:F5#
···········
𝄢:--- 𝄞:---
𝄢:--- 𝄞:---
𝄢:--- 𝄞:---
𝄢:--- 𝄞:---

录音文件

暂时没有。。。

源代码

GitHub仓库：sdl-wave-demo

参考

The Math Behind Music and Sound Synthesis

标签：钢琴 · 音频 · SDL · 五线谱